Notes on DDPG
Published:
Deep Deterministic Policy Gradient (DDPG) [1], is a model-free RL algorithm for continuous action spaces. It adopts an off-policy actor-critic approach and uses deterministic policies.
DDPG mainly draws from two previous papers, Deep Q Networks (DQN) [2] and Deterministic Policy Gradients (DPG) [3].
DQN
DQN combined deep learning and RL successfully for the first time and trained an agent to play atari video games using just pixels as input. DQN is based on the Q-learning algorithm [4], a popular off-policy algortihm which learns a greedy policy while following a exploratory behaviour policy (e.g $\epsilon$-greedy). DQN adapts Q-learning to use deep neural networks. To achieve stable learning while using large, non-linear function approximators, DQN uses two main innovations,
- Experience replay : the network is trained off-policy with samples from a replay buffer to minimize correlation between samples.
- Target networks : use a target Q-network to give consistent targets during temporal difference backups.
The loss function used to train the Q-network is given by, \[ L(w) = \underset{(s,a,r,s’)\sim D}{\mathbb{E}} [\; ( r + \gamma \max_{a’} Q^{w’}(s’,a’) - Q^{w}(s,a) )^{2} \;] \] It’s gradient is given by, \[ \nabla_{w} L(w) = \underset{(s,a,r,s’)\sim D}{\mathbb{E}} [\; - 2 \, ( r + \gamma \max_{a’} Q^{w’}(s’,a’) - Q^{w}(s,a) ) \nabla_{w} Q^{w}(s,a) \;] \] It is not possible to directly apply DQN to problems with continuous action spaces, as the Q-learning update requires computing a maximum over the action space, which in the case of continuous actions would require an iterative optimization process for every update.
DDPG instead adopts an actor-critic approach based on the DPG algorithm.
DPG
The DPG paper compares different policy gradient algorithms for reinforcement learning on continuous action spaces. DPG showed for the first time that the deterministic policy gradient actually exists and that it is simply the expected gradient of the action value function.
\[\begin{align} \nabla_{\theta} J(\mu_{_{\theta}}) &= \int_{\mathcal{S}} \rho^{\mu}(s) \nabla_{\theta} \mu_{_{\theta}}(s)\nabla_{a} Q^{\mu}(s,a)|_{a=\mu_{_{\theta}}(s)} ds \notag \\ &= \mathbb{E}_{s \sim \rho^{\mu}}[\nabla_{\theta} \mu_{_{\theta}}(s)\nabla_{a} Q^{\mu}(s,a)|_{a=\mu_{_{\theta}}(s)}] \notag \\ &= \mathbb{E}_{s \sim \rho^{\mu}}[\nabla_{\theta} Q^{\mu}(s,\mu_{_{\theta}}(s))] \notag \end{align}\]In comparison, the stochastic policy gradient which was first derived in [5] is given by,
\[\begin{align} \nabla_{\theta} J(\pi_{_{\theta}}) &= \int_{\mathcal{S}} \rho^{\pi}(s) \int_{\mathcal{A}} \nabla_{\theta} \pi_{_{\theta}}(a|s)\, Q^{\pi}(s,a) \, da \, ds \notag \\ &= \mathbb{E}_{s \sim \rho^{\pi}, a \sim \pi_{_{\theta}}}[\nabla_{\theta} \log\pi_{_{\theta}}(a|s)\, Q^{\pi}(s,a)] \notag \end{align}\]DPG argues that the deterministic policy gradient can be estimated much more efficiently (with fewer samples) compared to the stochastic policy gradient, as the former requires an integration over only the state space, while the latter requires an integration over both the state and action spaces. This is especially true when the action space has many dimensions.
DPG then states that a standalone deterministic policy cannot be used, as it will not be able to explore adequately, which will lead to sub-optimal solutions. An off-policy approach is needed, where a stochastic behaviour policy $\beta$ is followed to ensure sufficient exploration, while learning about a deterministic target policy $\mu$, exploiting the efficiency of the deterministic policy gradient. DPG shows that the off-policy deterministic policy gradient is given by,
\[\begin{align} \nabla_{\theta} J_{\beta}(\mu_{_{\theta}}) &\approx \int_{\mathcal{S}} \rho^{\beta}(s) \nabla_{\theta} \mu_{_{\theta}}(s)\nabla_{a} Q^{\mu}(s,a)|_{a=\mu_{_{\theta}}(s)} ds \notag \\ &= \mathbb{E}_{s \sim \rho^{\beta}}[\nabla_{\theta} \mu_{_{\theta}}(s)\nabla_{a} Q^{\mu}(s,a)|_{a=\mu_{_{\theta}}(s)}] \notag \end{align}\]DDPG
DDPG adapts DPG to use deep neural networks. To ensure stability while training with deep neural networks, DDPG uses the ideas underlying the success of DQN such as experience replay and target networks. To work with observations containing different physical quantities (e.g position, velocity), whose ranges may vary across environments, DDPG uses batch normalization. The overall DDPG algorithm is summarized below.

Implementation
You can find my Pytorch implementation of DDPG here.
Results
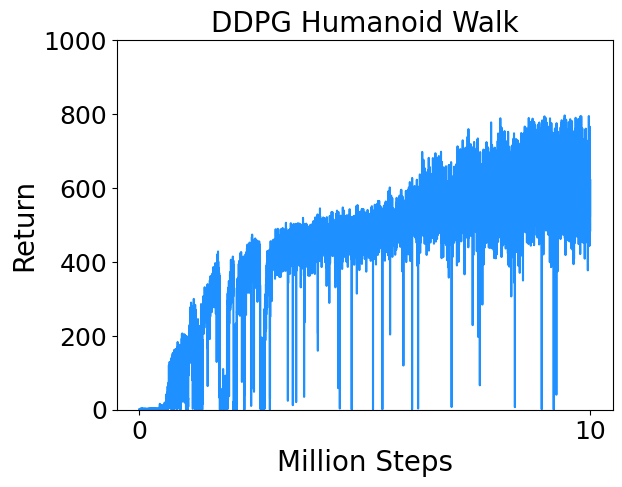
I trained DDPG on a few continuous control tasks from Deepmind Control Suite. Results are below.
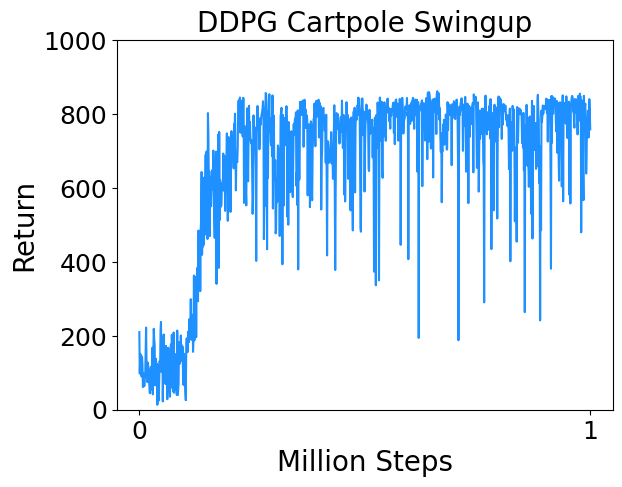
- Cartpole Swingup : Swing up and balance an unactuated pole by applying forces to a cart at its base.

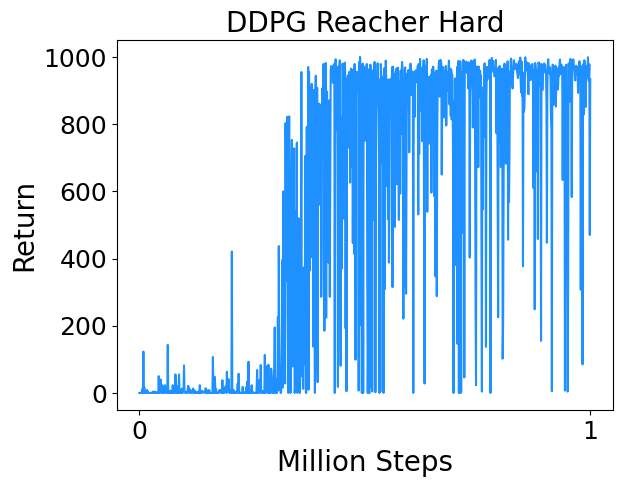
- Reacher Hard : Control a two-link robotic arm to reach a random target location.

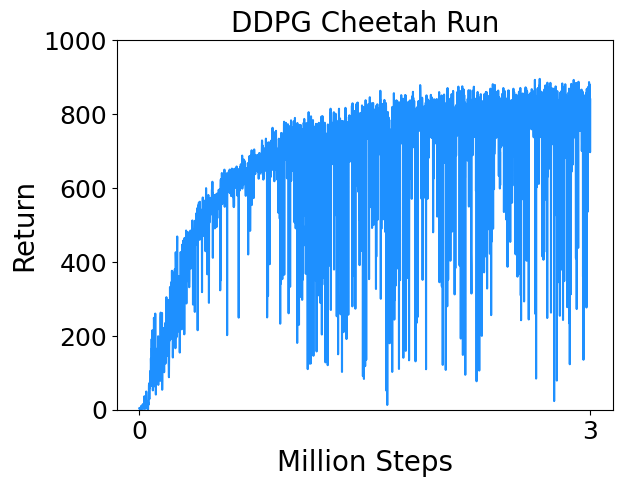
- Cheetah Run : Control a planar biped to run.

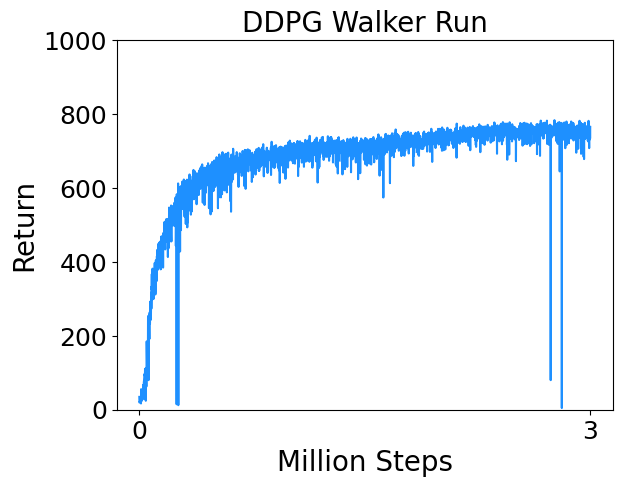
- Walker Run : Control a planar biped to run.

- Humanoid Walk : Control a simplified humanoid to walk.

References
[1] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971, 2015. Link
[2] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602, 2013.
[3] David Silver, Guy Lever, Nicolas Heess, Thomas Degris, Daan Wierstra, and Martin Riedmiller. Deterministic policy gradient algorithms. In International conference on machine learning, pages 387–395. PMLR, 2014.
[4] Christopher JCH Watkins and Peter Dayan. Q-learning. Machine learning, 8(3):279–292, 1992.
[5] Richard S Sutton, David McAllester, Satinder Singh, and Yishay Mansour. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems, 12, 1999.