Random Walk

1 minute read

Published:

Consider the classic random walk problem. Let $N$ states be laid out in a row, with the left most state being a terminal state. Consider an agent who, when at a non-terminal state, chooses to move with probability $p$ to the left neighbour and with probability $1-p$ to the right neighbour (or to itself in case of the right-most state). All rewards are 1. Our objective is to estimate the expected return from each state, under the agent’s policy.

MDP definition

  • State Space

    Set of all states, including terminal state, $\mathcal{S}^{+} = \{1,2…,N\}$.

    Set of all states, excluding terminal state, $\mathcal{S} = \{2…,N\}$.

  • Action Space

    For all $s\in S$, set of valid actions at $s$,

\[\mathcal{A}(s) = \begin{cases} \{-1,0\} \text{ if } s = N \\ \{-1,1\} \text{ if } s \in S-\{N\} \end{cases} \nonumber\]

  • Reward Structure

    For all $s \in \mathcal{S}, \ a \in \mathcal{A}(s)$,

\[\mathcal{R}(s,a) = \mathbb{E}[R_{t+1}|S_{t}=s,A_{t}=a ]= 1 \nonumber\]

  • Transition Model

    For all $ s \in \mathcal{S}, \ a \in \mathcal{A}(s),s’ \in \mathcal{S}^{+}$,

\[\mathcal{P}(s,a,s')= \mathbb{P}[S_{t+1}=s'|S_{t}=s,A_{t}=a ] = \begin{cases} 1 \text{ if } s'= s+a \\ 0 \text{ if } s' \in S^{+}-\{s+a\} \end{cases} \nonumber\]

Agent’s Policy

For all $ s \in \mathcal{S}, \ a \in \mathcal{A}(s)$,

\[\pi_{agent}(s,a) = \mathbb{P}[A_{t}=a |S_{t}=s] = \begin{cases} \text{ if } s = N \ \begin{cases} p \text{ if } a = -1 \\ 1-p \text{ if } a = 0 \end{cases} \\ \text{ if } s \in \mathcal{S}-\{N\} \ \begin{cases} p \text{ if } a = -1 \\ 1-p \text{ if } a = 1 \end{cases} \end{cases} \nonumber\]

Objective : Evaluate $v_{\pi_{agent}}$. Assume $N=11, \ p = 0.7, \ \gamma = 1$.

In the solutions to follow, we store the Value function V in a table since the State and Action Spaces are discrete and finite.

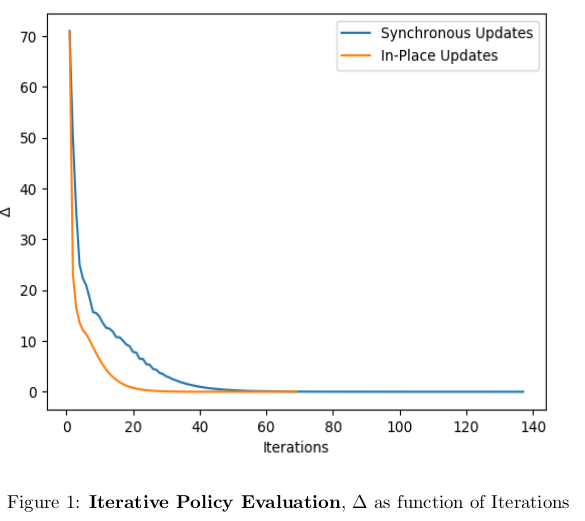
Model Based Policy Evaluation

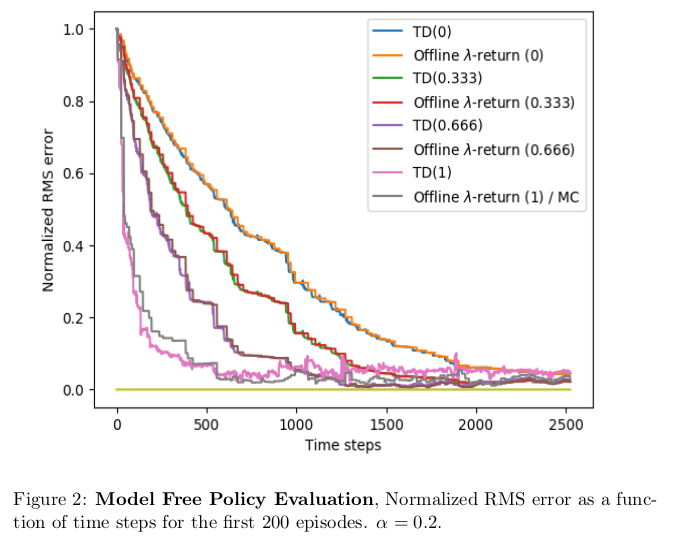
Model Free Policy Evaluation

You can find the code used in these experiments here.