Notes on Soft Actor-Critic
Published:
Soft Actor-Critic (SAC) [1] [2] is a state-of-the-art model-free RL algorithm for continuous action spaces. It adopts an off-policy actor-critic approach and uses stochastic policies. It uses the maximum entropy formulation to achieve better exploration.
Maximum Entropy RL
In maximum entropy RL, the objective is to maximize the expected return while acting as randomly as possible. By doing so, the agent can explore better and capture different modes of optimality. This also improves robustness against environmental changes.

An agent trained using the maximum entropy RL objective explores both passages during training.
The entropy of a random variable is given by, $H(X) = \underset{x \sim P}{\mathbb{E}}[-\log P(x)] $. Thus, we define the maximum entropy RL objective as, \[ \pi^{*} = \underset{\pi}{\arg\max} \underset{\tau \sim \pi}{\mathbb{E}} \big[\sum_{t=0}^{\infty}\gamma^{t}\big(\;r(s_{t},a_{t},s_{t+1})+\alpha H(\pi(\cdot|s_{t}))\;\big)\big] \]
Here, $\alpha > 0$, is the weightage given to the entropy term in the objective. $\alpha$ is also referred to as the “temperature”. We define the value function to include the entropy from every timestep, \[ V^\pi(s) = \underset{\tau \sim \pi}{\mathbb{E}}\big[\sum_{t=0}^{\infty}\gamma^{t}\big(\;r(s_{t},a_{t},s_{t+1})+\alpha H(\pi(\cdot|s_{t}))\;\big)\;\big|\;s_{0}=s\,\big] \]
We define the action-value function to include the entropy from every timestep except the first, \[ Q^\pi(s,a) = \underset{\tau \sim \pi}{\mathbb{E}}\big[\sum_{t=0}^{\infty}\gamma^{t} r(s_{t},a_{t},s_{t+1}) + \alpha \sum_{t=1}^{\infty} \gamma^{t} H(\pi(\cdot|s_{t})) \;\big|\;s_{0}=s,a_{0}=a\,\big] \]
Thus, \[ V^\pi(s) = \underset{a \sim \pi}{\mathbb{E}}[Q^\pi(s,a)] + \alpha H(\pi(\cdot|s)) \]
SAC
In SAC, we have,
- a single policy network, $ \pi_{\theta} $
- two Q networks $Q_{w_{1}} \; , \; Q_{w_{2}}$
- two target Q networks $Q_{w_{1}^{‘}} \; , \; Q_{w_{2}^{‘}}$
We train both Q-functions to regress a single shared target y, which is computed using target Q-networks and makes use of the clipped double-Q trick. \[y = r + \gamma \; (\; \underset{i=1,2}{\min} Q_{w_{i}^{‘}}(s’,a’) - \alpha \log \pi_{\theta}(a’|s’) \;)\]
The next-state actions used in the target come from the current policy instead of the target policy. The loss function is given by, \[L(w_{i}) = \underset{(s,a,r,s’)\sim \mathcal{D}}{\mathbb{E}}[\;( Q_{w_{i}}(s,a)-y )^{2}\;]\]
In policy learning, the objective is to maximize, \[ V^\pi(s) = \underset{a \sim \pi}{\mathbb{E}}[Q^\pi(s,a)] + \alpha H(\pi(\cdot|s)) \]
The policy is stochastic, therefore actions are sampled. To be able to backpropagate through sampled actions, we use the reparameterization trick. The policy outputs the mean $\mu$ and standard deviation $\sigma$ of a Gaussian distribution. We then sample a gaussian noise $\epsilon \sim \mathcal{N}(0,\mathbb{I})$. We then combine the noise with the policy outputs and use tanh to squash the action to [-1,1]. \[ a = a_{\theta}(s,\epsilon) = \text{tanh}(\mu_{\theta}(s)+\sigma_{\theta}(s)\cdot \epsilon) \]
We rewrite the expectation over actions in the objective into an expectation over noise, \[ \underset{a\sim \pi_{\theta}}{\mathbb{E}}[\; Q^{\pi_{\theta}}(s,a) - \alpha \log \pi_{\theta}(a|s) \;] = \underset{\epsilon \sim\mathcal{N}}{\mathbb{E}}[\; Q^{\pi_{\theta}}(s,a_{\theta}(s,\epsilon)) - \alpha \log \pi_{\theta}(a_{\theta}(s,\epsilon)|s) \;] \]
Thus, the objective becomes, \[ \underset{\theta}{\max} \underset{\epsilon \sim\mathcal{N}}{\underset{s\sim \mathcal{D}}{\mathbb{E}}} [\; (\; \underset{i=1,2}{\min} Q_{w_{i}}(s,a_{\theta}(s,\epsilon)) - \alpha \log \pi_{\theta}(a_{\theta}(s,\epsilon)|s) \;] \]
Algorithm

In SAC v1, the temperature $\alpha$ is a hyperparameter. However it was found that the algorithm is brittle to the choice of $\alpha$. In SAC v2, the temperature $\alpha$ is learnt by minimizing the loss, \[ L(\alpha) = \alpha \; (-\log\pi(a|s)-\widetilde{H}) \]
where $\widetilde{H}$ is the entropy target. Typically, $\widetilde{H}$ is set to be equal to the negative of the action space dimension i. e. $\widetilde{H} = - \; \text{dim}(\mathcal{A})$.
Implementation
You can find my Pytorch implementation of SAC for continuous action spaces here.
Results
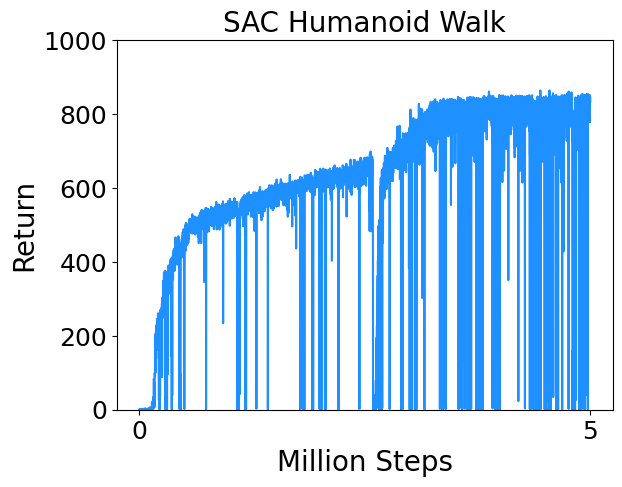
I trained SAC on a few continuous control tasks from Deepmind Control Suite. Results are below.
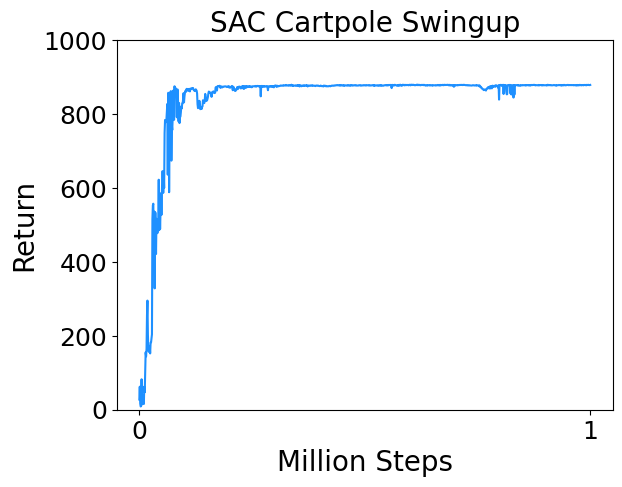
- Cartpole Swingup : Swing up and balance an unactuated pole by applying forces to a cart at its base.

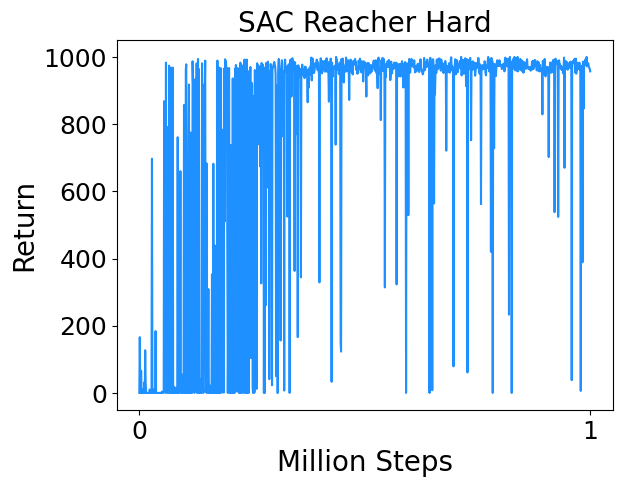
- Reacher Hard : Control a two-link robotic arm to reach a random target location.

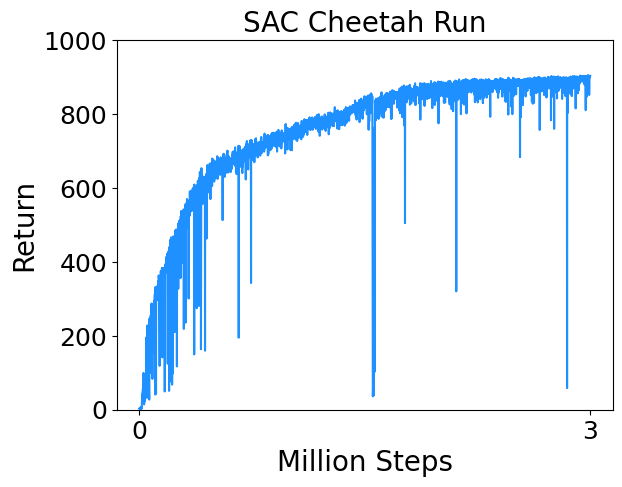
- Cheetah Run : Control a planar biped to run.

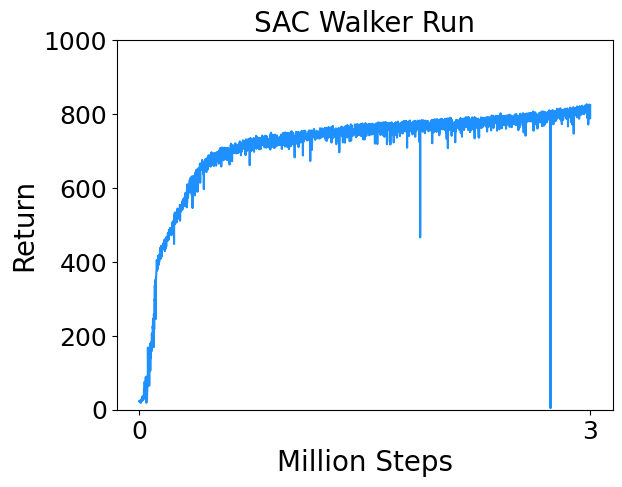
- Walker Run : Control a planar biped to run.

- Humanoid Walk : Control a simplified humanoid to walk.

References
[1] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In International conference on machine learning, pages 1861–1870. PMLR, 2018a. Link
[2] Tuomas Haarnoja, Aurick Zhou, Kristian Hartikainen, George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar, Henry Zhu, Abhishek Gupta, Pieter Abbeel, et al. Soft actor-critic algorithms and applications. arXiv preprint arXiv:1812.05905, 2018b. Link