Mixed State Entanglement In Quantized Chaotic Systems

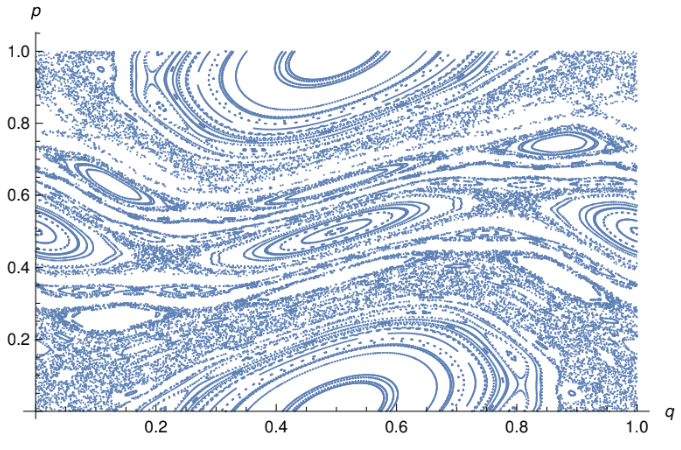
This work represents my master’s thesis carried out at IIT Madras, with Prof. Arul Lakshminarayan. We studied the connections between chaos and quantum entanglement. In particular, we studied entanglement in mixed states of quantized chaotic systems, focusing on the quantum coupled standard map. We studied its entanglement dynamics for different interaction strengths and environment dimensions. We identified a critical dimension where entanglement decreases, potentially posing challenges in applications like quantum computing.

You can view my complete thesis here.

Summary

Many physical systems in nature, for example, all atoms and molecules except the hydrogen atom (and related two-body atomic systems) exhibit chaos when treated classically [1] [2]. The same atoms and molecules when treated quantum mechanically, exhibit quantum chaos [3]. Decoherence, which explains wavefunction collapse as the quantum nature of a system “leaks” into it’s environment, is strongly influenced by chaos in the system / environment [4]. Also, quantum chaos is known to have an important place in the foundation of quantum statistical mechanics [5]. Thus, the study of quantum chaos becomes important from a general quantum mechanical perspective.

Quantum entanglement is a physical phenomenon where, many particles interact in ways such that, given a quantum state for the system as a whole, each particle cannot be assigned a single state vector [6]. Entanglement has been part of the foundational discussions of quantum mechanics since the time of Schrodinger [7] (who gave it it’s name) and the famous EPR paper of Einstein, Podolski and Rosen [8]. Entanglement is a topic of extensive contemporary research due to it’s newly found applications to quantum information and quantum computation [6].

Quantum chaos is known to impact entanglement in a non trivial manner [9]. Whether it will potentially aid or hinder a quantum computer remains unanswered. Almost all previous work on entanglement in quantized chaotic systems have dealt only with pure states, either stationary states (eigenstates) or other time evolved non-stationary pure states. In reality, even a carefully prepared and isolated system tends to interact with its environment, which has the effect of leaving the system in a mixed state. Thus, the study of mixed state entanglement in quantized chaotic systems forms an important and unexplored problem and forms the focus of this study.

We consider a prototypical system, the standard map [10] [11], which is essentially a periodically kicked pendulum. It is a simple system that exhibits classical chaos for certain values of its parameters. We let two standard maps interact through a potential to obtain a coupled standard map. We then quantize the coupled standard map to obtain the quantum coupled standard map, which is our system of interest. We study its entanglement under time evolution for initial states that are mixed, for different interaction strengths between the standard maps and different dimensions of the surrounding environment. We find that, for a given interaction strength, as we increase the environment dimension, the tendency to get entangled reduces and there exists a critical dimension in most cases, beyond which the state remains separable at all times. Such a phenomenon is potentially a problem in situations where entanglement is desirable, such as in quantum computing.

References

[1] Blümel, R., & Reinhardt, W. P. (1997). Chaos in atomic physics (No. 10). Cambridge University Press.

[2] Gutzwiller, M. C. (2013). Chaos in classical and quantum mechanics (Vol. 1). Springer Science & Business Media.

[3] Porter, M. A. (2001). An introduction to quantum chaos. arXiv preprint nlin/0107039.

[4] Zurek, W. H., & Paz, J. P. (1994). Decoherence, chaos, and the second law. Physical Review Letters, 72(16), 2508.

[5] Srednicki, M. (1994). Does quantum chaos explain quantum statistical mechanics?. arXiv preprint cond-mat/9410046.

[6] Horodecki, R., Horodecki, P., Horodecki, M., & Horodecki, K. (2009). Quantum entanglement. Reviews of modern physics, 81(2), 865.

[7] Schrödinger, E. (1935, October). Discussion of probability relations between separated systems. In Mathematical Proceedings of the Cambridge Philosophical Society (Vol. 31, No. 4, pp. 555-563). Cambridge University Press.

[8] Einstein, A., Podolsky, B., & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete?. Physical review, 47(10), 777.

[9] Lakshminarayan, A. (2001). Entangling power of quantized chaotic systems. Physical Review E, 64(3), 036207.

[10] Chririkov, B. V. (1979). A universal instability of many-dimensional oscillators systems. Phys Rep, 52, 265.

[11] Lichtenberg, A. J., & Lieberman, M. A. (2013). Regular and chaotic dynamics (Vol. 38). Springer Science & Business Media.